Средновековният търговец-математик Леонардо Фибоначи от Пиза е автор на загубеният трактат "Kнига за абака"(книга за изчисления), който определя развитието математиката в Европа за няколко столетия. Именно в този трактат европейците се запознали с индуските (арабските) цифри.

Днес Леонардо от Пиза е известен благодарение на френския математик Люка, който нарекъл на името на Фибоначи числовата последователност, възникнала в една доста тривиална задачка от легендарния трактат:

"Някой си поместил двойка зайци на накакво място, обградено от всички страни със стена, за да разбере колко двойки зайци ще се родят в течение на година, ако природата на зайците е такава, че след месец двойката зайци ще възпроизведе на бял свят друга двойка, а зайците ще могат да раждат други зайчета от втория месец след своето раждане".

На шестия месец— 5+3=8 двойки (защото потомство дават само тези двойки, които са родени на четвъртия месец) и т.н.

Ако означим броя двойки зайци на n-тия месец с F_n , то F₁=1, F₂=1, F₃=2, F₄=3, F₅=5, F₆=8, F₇=13, F₈=21 и т.н. или:
    F_n=F_n-1+F_n-2, за всички n>2.
Броят на двойките зайци на n-тия месец е равен на броя F_n-1двойки зайци от миналия месец плюс броят на родилите се двойки зайци, който съвпада с числото F_n-2 двойки зайци, родили през (n-2)-рия месец (нали само те даваха потомство).

Числа F_n, образуващи последователността 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... се наричат "числа на Фибоначи", а самата последователност — ред на Фибоначи.

Коефициенти на Фибоначи и "златното число"

Едно от най-важните свойства на числата на Фибоначи е съществуването на т.н. коефициенти на Фибоначи, т.е. постоянни отношения на различни членове на реда. Те се определят по следния начин:

• Отношението на всяко число към следващото, което се стреми все повече и повече към 0.61803...
• Отношението на всяко число към предишното се стреми към 1.61803... (обратно на 0.618). Числото 1.61803... , по точно ,е прочутото ирационално число, наречено златно сечение и ще му отделим внимание в отделна тема. Означава се с главната гръцка буква Ф (фи).

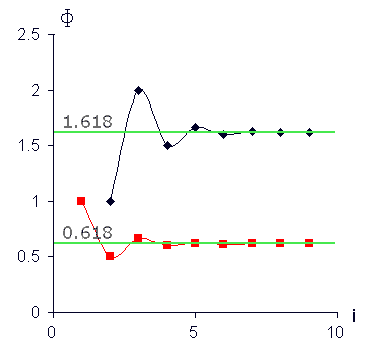При делене на всяко число на следващото през едно получаваме числото 0.382; и обратно – съответно 2.618. Подбирайки по такъв начин отношения, получаваме основния набор от коефициентите на Фибоначи: … 4.235, 2.618, 1.618, 0.618, 0.382, 0.236, също и 0.5 (1/2). Всички те играят особена роля в природата.

Числата на на Фибоначи имат още куп удивителни свойства, които са разгледани подробно в книгите на М. Гарднер "Математически развлечения".

Правоъгълници и спирали на Фибоначи

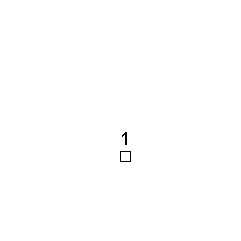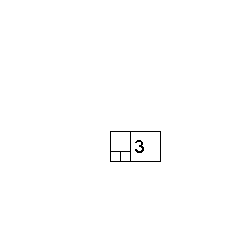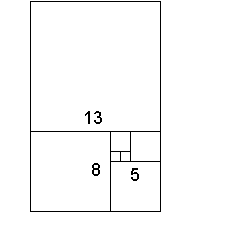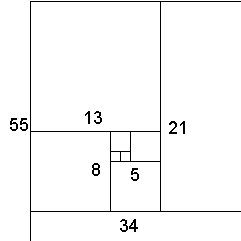Можем да направим друго изображение, показващо реда на Фибоначи 1,1,2,3,5,8,13,21 като започнем с два малки квадрата с размер 1/1 един до друг. На общата им страна се построява квадрат с размер 2/2 (=1+1). Сега можем да направим нов квадрат със страна, допираща се до последния квадрат със страна 2 и до първия- новия ще има страна 3, следващия, допиращ се до квадрат 2 и до квадрат 3 ще има страна 5 и т.н.. Можем да продължим да добавяме квадрати около изображението и всеки нов квадрат, ще има страна, която ще бъде сума от последните две страни на квадрати. Тази група правоъгълници, чиито страни имат дължина две последователни числа на Фибоначи и която се формира от квадрати със страни, които са числа на Фибоначи, се наричат правоъгълници на Фибоначи.

.Ако във всеки от горните квадрати впишем по четвърт кръг, ще получим спиралата на Фибоначи. Тази спирала не е истинска математическа логаритмична спирала, защото се съставя от фрагменти, но е добро приближение.

Наричат я още спирала на Бернули, логаритмическа спирала, равноъгълна спирала, и др. Такива спирали може да видим във формата на черупките на някои мекотели, а също и в подредбата на семената на цветовете на някои растения, семенниците на шишарките, ананаса, ухото и много други образувания. И коефициента на нарастване е често близък до 1.618.

Тази спирала е единствената, която запазва формата си при увеличаване на размерите. Това нейно свойство обяснява широкото и разпространение в природните образувания. Например, когато охлювът Nautflus расте, неговата раковина, разделена с вътрешни преградни стенички, увеличава размерите си, като се навива по спирала. При това черупката на охлюва не променя формата си, ако увеличиме машаба. Подобни форми могат да се наблюдават както при галактиктиките и атмосферните явления, така и доста често в растителния и животински свят.

Това свойство може да се нарече "самоподобие" и има пряка връзка с фракталите.

Mагията на числата на Фибоначи

Ако се разровите из Интернет, търсейки нещо за Фибоначи, ще попаднете на повече финансови сайтове, отколкото на математически. Забелязано е, че вълните, описващи колебанията на котировките на ценните книжа, съответстват на реда на Фибоначи и ги наричат вълни на Елиот.

След редица доста успешни удари на борса Ралф Елиот публикувал през 1939 г. серия статии в Financial World Magazine. В тях за първи път била представена теорията му, че движението на индекса Доу-Джонс се подчинява на определен ритъм. Излиза, че числата на Фибоначи могат да Ви направят и богати. Ако някой желае, да ми пише - мога да напиша тема и за вълните на Елиот.

Ще ми се да завърша с думите на самият Елиот: "На всяка човешка дейност са присъщи три отличителни особености: форма, време и отношение - и всичките те се подчиняват на реда на Фибоначи".

wmileva.hit.bg